| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- QGIS다운로드
- GIS
- 2023다이어리
- python
- xy좌표
- 그리드생성
- SHP
- 단계구분
- shp파일
- 오픈더도아
- 속성테이블편집
- QGIS
- QGIS3.22
- 대한민국shp
- 굿노트무료
- 읍면동shp
- 도형수정
- 속성테이블
- 다중부분을단일부분으로
- wsg4326
- 스크래치레이어
- shapefile
- 누적막대그래프
- 공간인덱스
- 누적막대차트
- QGIS분석
- 폴리곤내점개수세기
- 행정구역shp
- GIS분석
- 레이어
- Today
- Total
Open the Doah !
《Data Science》 데이터 과학을 위한 통계 1.3 본문
study - 데이터 과학을 위한 통계

1.3 위치 추정
데이터를 살펴보는 가장 기초적인 단계는 각 피처 (변수)의 '대표값 typical value'을 구하는 것이다
이는 대부분의 값이 어디쯤에 위치하는지 (중심경향성)를 나타내는 추정값이다
🔎용어 정리
- 평균 mean : 모든 값의 총합을 개수로 나눈 값 (유의어 : 평균 average)
- 가중평균 weighted mean : 가중치를 곱한 값의 총합을 가중치의 총합으로 나눈 값 (유의어 : 가중평균 weighted average)
- 중간값 median : 데이터에서 가장 가운데 위치한 값 (유의어 : 50번째 백분위수 percentile)
- 가중 중간값 weighted median : 데이터를 정렬한 후, 각 가중치 값을 위에서부터 더할 때, 총합의 중간이 위치하는 데이터 값
- 절사 평균 trimmed mean : 정해진 개수의 극단값 extreme value 을 제외한 나머지 값들의 평균 (유의어 : 절단평균 truncated mean)
- 로버스트하다 robust : 극단값들에 민감하지 않다는 것을 의미한다. (유의어 : 저항성 있다 resistant)
- 특이값 outlier : 대부분의 값과 매우 다른 데이터 값 (유의어 : 극단값)
데이터를 요약하려면 데이터의 평균을 구하면 되지 않냐고 생각할 수 있지만, 평균이 데이터의 중간을 대표하는 가장 좋은 방법은 아니다.
몇 가지 이유로, 통계학자들은 평균을 대체할 만한 다른 값들을 개발해냈다
🗒️ NOTE 측정 지표와 추정값
통계학자들은 보통 데이터로부터 얻은 값과 실제 상태를 나타내는 이론적인 참값을 구분하기 위해, 데이터로 부터 계산된 값들을 보통 추정값 estimate 이라는 용어를 사용한다.
반면 데이터 과학자나 비즈니스 분석가들은 이러한 값들을 측정 지표 metric 라고 부른다. 이러한 차이는 곧 통계학과 데이터 과학의 접근법의 차이를 반영한다.
통계학이라는 분야는 궁극적으로 불확실성을 이해하고자 하는 반면, 데이터 과학은 구체적인 비즈니스나 조직의 목표치에 관심을 둔다.
그러므로, 통계학자들은 추정한다고 하고 데이터 과학자들은 측정한다고 한다.
1.3.1 평균
평균은 가장 기본적인 위치 추정 방법
평균은 모든 값의 총합을 값의 개수로 나눈 값이다
x_bar : 모집단 표본의 평균
n개의 값, 즉 x1, x2, ... , xn 의 평균을 계산하는 수식은 다음과 같다

🗒️ NOTE
N (혹은 n)은 주로 레코드나 관측값의 개수를 나타낸다. 통계학에서 대문자는 모집단을, 소문자는 모집단에서 얻은 표본의 개수를 의미한다. 이러한 구분이 그렇게 중요하지 않은 데이터 과학에서는 모두 같은 의미로 사용한다
평균을 변형한 것 중 하나로 절사평균이 있다. 절사평균은 값들을 크기 순으로 정렬한 후, 양끝에서 일정 개수의 값들을 삭제한 뒤 남은 값들을 가지고 구한 평균을 말한다.
정렬한 값들이 x(1),x(2), ... , x(n)이라 할 때, 즉 x(1)이 가장 작은 값, x(n)이 가장 큰 값을 의미할 때, p개의 가장 크고 작은 값들을 제외한 뒤 절사평균을 계산하는 수식은 다음과 같다
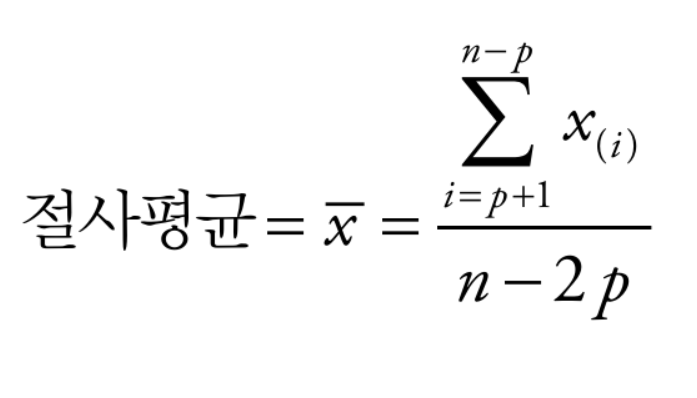
절사평균은 극단값의 영향을 제거한다. 예를 들어 다이빙 대회에서는 5명의 심판이 매긴 점수 중에서 가장 높은 점수와 낮은 점수를 제외한 나머지 3명의 점수를 평균한 값으로 최종 성적을 매긴다.
혹시 한 심판이 자국의 선수 등에게 유리한 심사를 하더라도, 이 심판이 전체 성적에 영향을 주기는 어렵다.
또 다른 종류의 평균으로, 각 데이터 값 x(i)에 가중치 w(i)를 곱한 값들의 총합을 다시 가중치의 총합으로 나눈 가중평균이 있다. 가중평균은 다음과 같은 수식으로 나타낼 수 있다.
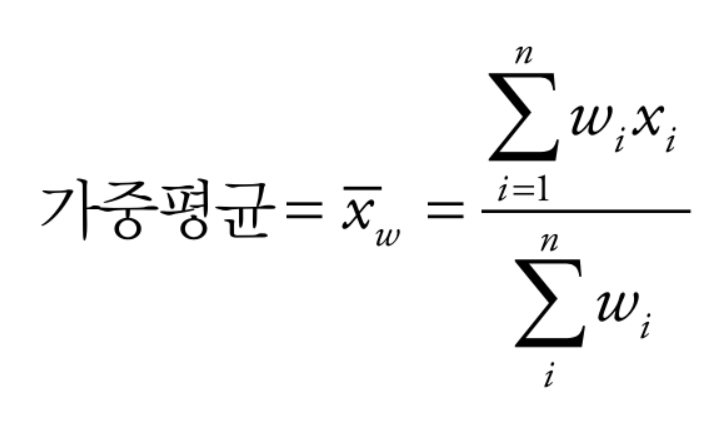
가중평균을 사용하게 된 두 가지 중요한 이유가 있다.
- 어떤 값들이 본래 다른 값들에 비해 큰 변화량을 갖을 때, 이러한 관측값에 대해 더 작은 가중치를 줄 수 있다. 예를 들어 여러 개의 센서로부터 평균을 구한다고 할 때, 한 센서의 정확도가 떨어진다면 그 센서에서 나온 데이터에는 낮은 가중치를 주는 것이 합리적일 것이다.
- 데이터를 수집할 때, 우리가 관심 있는 서로 다른 대조군에 대해서 항상 똑같은 수가 얻어지지는 않는다. 예를 들어 온라인 실험을 진행할 때, (방법에 따라 다르겠지만) 모든 사용자 그룹에 대해 정확히 같은 비율을 반영하는 데이터를 수집하기는 참 어렵다. 이를 보정하기 위해서, 데이터가 부족한 소수 그룹에 대해 더 높은 가중치를 적용할 필요도 있을 것이다.
1.3.2 중간값과 로버스트 추정
데이터를 일렬로 정렬했을 때, 한가운데에 위치하는 값을 중간값이라고 한다.
만약 데이터 개수가 짝수라면 그 중간값은 실제 데이터 값이 아닌 가운데 있는 두 값의 평균으로 한다.
모든 관측치를 다 사용하는 평균과는 달리, 중간값은 정렬된 데이터의 가운데에 위치한 값들만으로 결정된다. 이런 점에서 중간값이 불리할 것처럼 보이지만, 데이터에 매우 민감한 평균보다는 중간값이 많은 경우 위치 추정에 더 유리하다.
시애틀에서 레이크 워싱텅 주변 동네의 기준이 되는 가계 소득을 알아본다고 하자. 메디나와 원더미어를 서로 비교한다고 하면, 메디나에 빌 게이츠가 살고 있기 때문에 평균은 매우 다르게 나올 것이다. 만약 중간값을 사용한다면 빌 게이츠가 얼마나 부자인지 상관없이 중간치는 매우 비슷하게 나올 것이다.
가중평균을 사용하는 이유와 마찬가지로, 가중 중간값을 사용할 수도 있다.
중간값을 계산할 때와 마찬가지로 먼저 데이터를 정렬한다. 각 데이터 값은 이에 해당하는 가중치를 가지고 있다. 가중 중간값은 단순히 가운데 위치한 값이 아닌, 어떤 위치를 기준으로 상위 절반의 가중치의 합이 하위 절반의 가중치의 합과 동일한 위치의 값이 된다. 중간값과 마찬가지로 가중 중간값 역시 특잇값에 로버스트하다.
특이값
중간값은 결과를 왜곡할 수도 있는 특잇값(극단값) 들의 영향을 받지 않으므로 로버스트한 위치 추정 방법이라고 알려져 있다. 특잇값은 어떤 데이터 집합에서 다른 값들과 매우 멀리 떨어져 있는 값들을 말한다.
특잇값은 앞서 빌게이츠의 예와 같이 데이터 값 자체가 유효하지 않다거나 잘못되었다는 뜻이 아니다. 물론 다른 단위의 값들이 섞여 있다거나, 센서에서 잘못된 값이 읽히는 등 에러 값들이 특이값으로 나타나기도 한다.
특잇값들이 이러한 에러 값들 이라면, 평균은 뭔가 잘못된 위치 추정을 할 수 있는 반면, 중간값은 여전히 설득력 있는 결과를 줄 것이다. 물론 어떤 경우든, 이러한 듯이값들을 확인하고 자세히 살펴볼 필요가 있다.
🗒️ NOTE
이상 검출
전형적인 데이터 분석에서 특이값들은 가끔 유익한 정보를 제공하기도하고, 때로는 골칫거리가 되기도 한다.
하지만 이와 반대로, 이상 검출 anomaly detection 에서는 대부분의 정상적인 데이터보다는 예외적으로 측정된 특이값들이 바로 주된 관심의 대상이 된다.
중간값만이 로버스트한 위치를 추정하는 유일한 방법은 아니다. 사실 절사평균 역시 특이값의 영향을 줄이기 위해 많이 사용된다. 예를 들어 데이터의 상위 하위 10% 를 잘라내는 방법은 데이터가 너무 작지만 않다면, 특이값으로부터 데이터를 보호할 수 있다.
절사평균은 중간값과 평균의 절충안이라고 볼 수 있다. 데이터의 특이값들로부터 로버스트하지만 위치 추정을 위해 더 많은 데이터를 사용한다
'DataScience' 카테고리의 다른 글
| 《Data Science》 데이터 과학을 위한 통계 1~1.2 (0) | 2022.11.13 |
|---|

